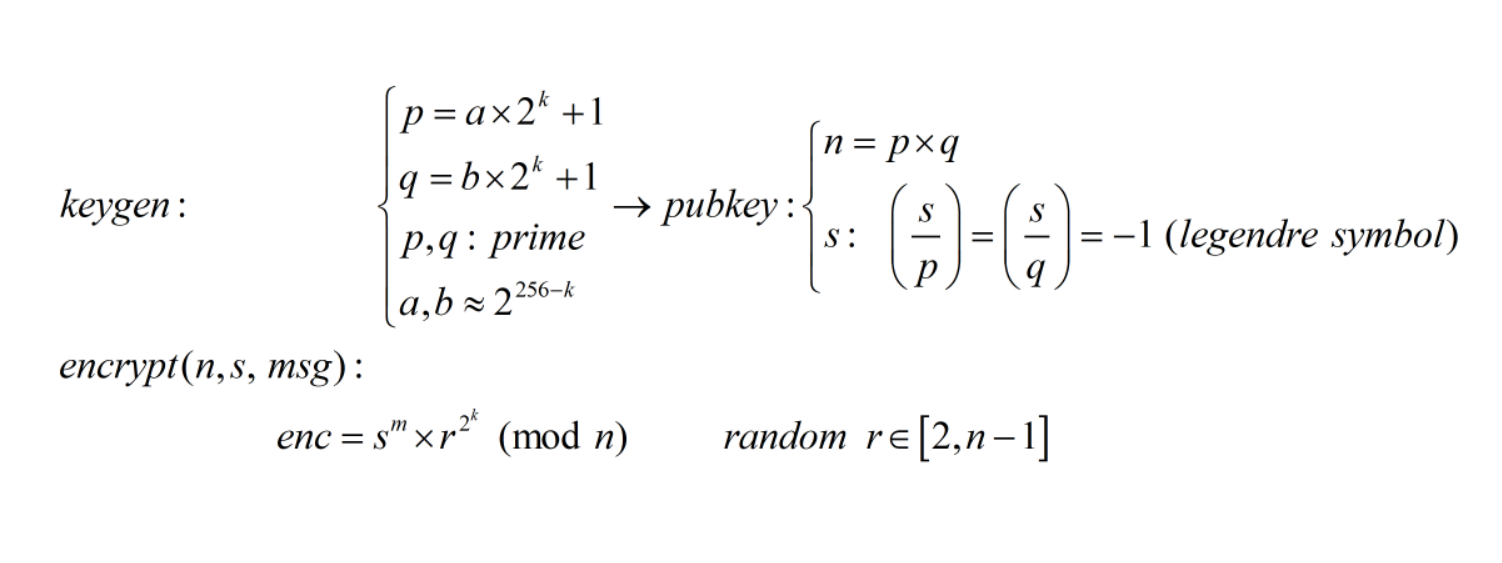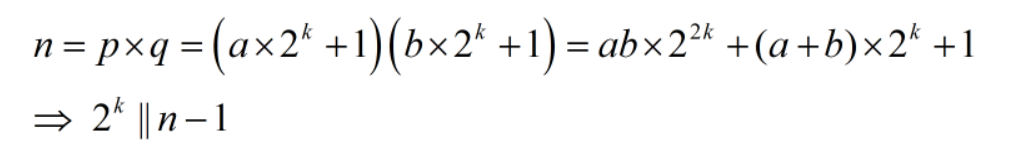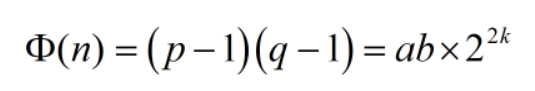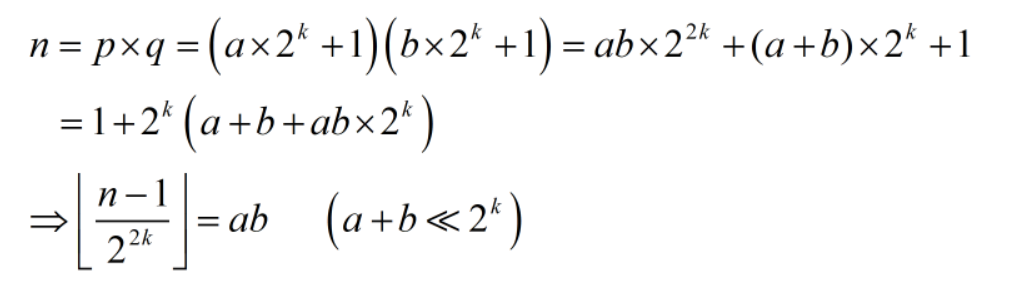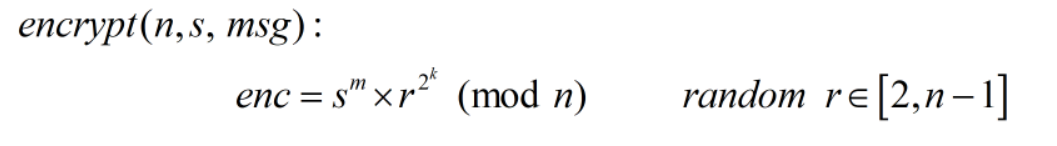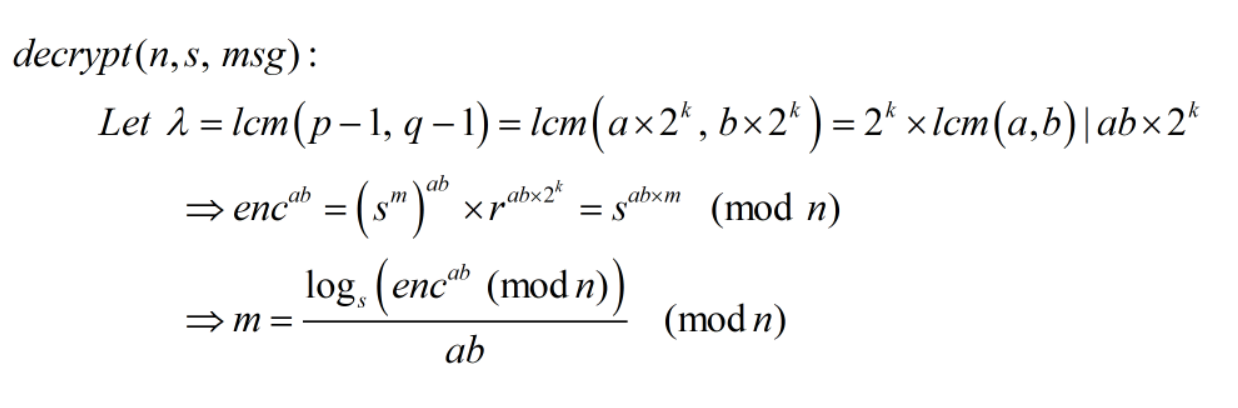Binned (126 solves, 45 points)
Description
People binned to the same public ID have no real-world connection to one another.Attachments
binned.py output.txt
Challenge overview
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
#!/usr/bin/env python3
from Crypto.Util.number import *
from gensafeprime import *
from flag import flag
def keygen(nbit):
p, q = [generate(nbit) for _ in range(2)]
return (p, q)
def encrypt(m, pubkey):
return pow(pubkey + 1, m, pubkey ** 3)
p, q = keygen(512)
n = p * q
flag = bytes_to_long(flag)
enc = encrypt(flag, n)
print(f'pubkey = {n}')
print(f'enc = {enc}')
1
2
pubkey = 125004899806380680278294077957993138206121343727674199724251084023100054797391533591150992663742497532376954423241741439218367086541339504325939051995057848301514908377941815605487168789148131591458301036686411659334843972203243490288676763861925647147178902977362125434420265824374952540259396010995154324589
enc = 789849126571263315208956108629196540107771075292285804732934458641661099043398300667318883764744131397353851782194467024270666326116745519739176492710750437625345677766980300328542459318943175684941281413218985938348407537978884988013947538034827562329111515306723274989323212194585378159386585826998838542734955059450048745917640814983343040930383529332576453845724747105810109832978045135562492851617884175410194781236450629682032219153517122695586503298477875749138129517477339813480115293124316913331705913455692462482942654717828006590051944205639923326375814299624264826939725890226430388059890231323791398412019416647826367964048142887158552454494856771139750458462334678907791079639005383932256589768726730285409763583606927779418528562990619985840033479201147509241313757191997545174262930707521451438204766627975109619779824255444258160
Ở bài này đại khái chúng ta sẽ đi giải phương trình
\[\begin{equation}\label{eq1} \left(n + 1\right)^{x} \equiv c \pmod{n^{3}} \tag{1} \end{equation}\]với $n, c$ là hai số cho trước và flag chính là $x$ cần tìm. Ta thử khai triển Newton phương trình $(1)$
Như vậy ta thu được phương trình đồng dư ẩn $x$, để ý rằng $n \sim 2^{1024}$ nên nếu $x < n$ thì ta có thể giải $(2)$ trên $\mathbb{Z}$ luôn (thay vì trên $\mathbb{Z}_{n^{2}}$)
Solution
1
2
3
4
5
6
7
8
from Crypto.Util.number import *
n = 125004899806380680278294077957993138206121343727674199724251084023100054797391533591150992663742497532376954423241741439218367086541339504325939051995057848301514908377941815605487168789148131591458301036686411659334843972203243490288676763861925647147178902977362125434420265824374952540259396010995154324589
c = 789849126571263315208956108629196540107771075292285804732934458641661099043398300667318883764744131397353851782194467024270666326116745519739176492710750437625345677766980300328542459318943175684941281413218985938348407537978884988013947538034827562329111515306723274989323212194585378159386585826998838542734955059450048745917640814983343040930383529332576453845724747105810109832978045135562492851617884175410194781236450629682032219153517122695586503298477875749138129517477339813480115293124316913331705913455692462482942654717828006590051944205639923326375814299624264826939725890226430388059890231323791398412019416647826367964048142887158552454494856771139750458462334678907791079639005383932256589768726730285409763583606927779418528562990619985840033479201147509241313757191997545174262930707521451438204766627975109619779824255444258160
x = (c%n**2 - 1)//n
flag = long_to_bytes(x)
print(flag)
Flag:
ASIS{8!N0miaL_3XpAn5iOn_Us4G3_1N_cRyp7o_9rApHy!}
Chaffymasking (66 solves, 73 points)
Description
Chaffy masking is a popular cryptography technique that is used to protect cryptographic implementations against several attacks.
nc 65.21.255.31 31377Attachments
chaffymasking.py
Challenge overview
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
#!/usr/bin/env python3
import numpy as np
import binascii
import os, sys
from flag import FLAG
def die(*args):
pr(*args)
quit()
def pr(*args):
s = " ".join(map(str, args))
sys.stdout.write(s + "\n")
sys.stdout.flush()
def sc():
return sys.stdin.buffer.readline()
def pad(inp, length):
result = inp + os.urandom(length - len(inp))
return result
def byte_xor(a, b):
return bytes(_a ^ _b for _a,_b in zip(a,b))
def chaffy_mask(salt, LTC, m, n):
q = n ** 2
half1_salt = salt[:m // 8]
half2_salt = salt[m // 8:]
xor_salts = int.from_bytes(byte_xor(half1_salt, half2_salt), "big")
if xor_salts == 0:
half1_salt = byte_xor(half1_salt, os.urandom(m))
half1_binStr = "{:08b}".format(int(half1_salt.hex(),16))
if(len(half1_binStr) < m):
half1_binStr = "0" * (m - len(half1_binStr)%m) + half1_binStr
half2_binStr = "{:08b}".format(int(half2_salt.hex(),16))
if(len(half2_binStr) < m):
half2_binStr = "0" * (m - len(half2_binStr)%m) + half2_binStr
vec_1 = np.array(list(half1_binStr), dtype=int)
vec_1 = np.reshape(vec_1, (m,1))
vec_2 = np.array(list(half2_binStr), dtype=int)
vec_2 = np.reshape(vec_2, (m,1))
out_1 = LTC.dot(vec_1) % q
out_2 = LTC.dot(vec_2) % q
flag_vector = np.array([ord(i) for i in FLAG])
flag_vector = np.reshape(flag_vector, (n,1))
masked_flag = (flag_vector ^ out_1 ^ out_2) % 256
masked_flag = np.reshape(masked_flag, (n,))
masked_flag = ''.join([hex(_)[2:].zfill(2) for _ in masked_flag])
return masked_flag.encode('utf-8')
def main():
border = "|"
pr(border*72)
pr(border, " Welcome to chaffymask combat, we implemented a masking method to ", border)
pr(border, " hide our secret. Masking is done by your 1024 bit input salt. Also ", border)
pr(border, " I noticed that there is a flaw in my method. Can you abuse it and ", border)
pr(border, " get the flag? In each step you should send salt and get the mask. ", border)
pr(border*72)
m, n = 512, 64
IVK = [3826, 476, 3667, 2233, 1239, 1166, 2119, 2559, 2376, 1208, 2165, 2897, 830, 529, 346, 150, 2188, 4025, 3667, 1829, 3987, 952, 3860, 2574, 959, 1394, 1481, 2822, 3794, 2950, 1190, 777, 604, 82, 49, 710, 1765, 3752, 2970, 952, 803, 873, 2647, 2643, 1096, 1202, 2236, 1492, 3372, 2106, 1868, 535, 161, 3143, 3370, 1, 1643, 2147, 2368, 3961, 1339, 552, 2641, 3222, 2505, 3449, 1540, 2024, 618, 1904, 314, 1306, 3173, 4040, 1488, 1339, 2545, 2167, 394, 46, 3169, 897, 4085, 4067, 3461, 3444, 118, 3185, 2267, 3239, 3612, 2775, 580, 3579, 3623, 1721, 189, 650, 2755, 1434, 35, 3167, 323, 589, 3410, 652, 2746, 2787, 3665, 828, 3200, 1450, 3147, 720, 3741, 1055, 505, 2929, 1423, 3629, 3, 1269, 4066, 125, 2432, 3306, 4015, 2350, 2154, 2623, 1304, 493, 763, 1765, 2608, 695, 30, 2462, 294, 3656, 3231, 3647, 3776, 3457, 2285, 2992, 3997, 603, 2342, 2283, 3029, 3299, 1690, 3281, 3568, 1927, 2909, 1797, 1675, 3245, 2604, 1272, 1146, 3301, 13, 3712, 2691, 1097, 1396, 3694, 3866, 2066, 1946, 3476, 1182, 3409, 3510, 2920, 2743, 1126, 2154, 3447, 1442, 2021, 1748, 1075, 1439, 3932, 3438, 781, 1478, 1708, 461, 50, 1881, 1353, 2959, 1225, 1923, 1414, 4046, 3416, 2845, 1498, 4036, 3899, 3878, 766, 3975, 1355, 2602, 3588, 3508, 3660, 3237, 3018, 1619, 2797, 1823, 1185, 3225, 1270, 87, 979, 124, 1239, 1763, 2672, 3951, 984, 869, 3897, 327, 912, 1826, 3354, 1485, 2942, 746, 833, 3968, 1437, 3590, 2151, 1523, 98, 164, 3119, 1161, 3804, 1850, 3027, 1715, 3847, 2407, 2549, 467, 2029, 2808, 1782, 1134, 1953, 47, 1406, 3828, 1277, 2864, 2392, 3458, 2877, 1851, 1033, 798, 2187, 54, 2800, 890, 3759, 4085, 3801, 3128, 3788, 2926, 1983, 55, 2173, 2579, 904, 1019, 2108, 3054, 284, 2428, 2371, 2045, 907, 1379, 2367, 351, 3678, 1087, 2821, 152, 1783, 1993, 3183, 1317, 2726, 2609, 1255, 144, 2415, 2498, 721, 668, 355, 94, 1997, 2609, 1945, 3011, 2405, 713, 2811, 4076, 2367, 3218, 1353, 3957, 2056, 881, 3420, 1994, 1329, 892, 1577, 688, 134, 371, 774, 3855, 1461, 1536, 1824, 1164, 1675, 46, 1267, 3652, 67, 3816, 3169, 2116, 3930, 2979, 3166, 3944, 2252, 2988, 34, 873, 1643, 1159, 2822, 1235, 2604, 888, 2036, 3053, 971, 1585, 2439, 2599, 1447, 1773, 984, 261, 3233, 2861, 618, 465, 3016, 3081, 1230, 1027, 3177, 459, 3041, 513, 1505, 3410, 3167, 177, 958, 2118, 326, 31, 2663, 2026, 2549, 3026, 2364, 1540, 3236, 2644, 4050, 735, 280, 798, 169, 3808, 2384, 3497, 1759, 2415, 3444, 1562, 3472, 1151, 1984, 2454, 3167, 1538, 941, 1561, 3071, 845, 2824, 58, 1467, 3807, 2191, 1858, 106, 3847, 1326, 3868, 2787, 1624, 795, 3214, 1932, 3496, 457, 2595, 3043, 772, 2436, 2160, 3428, 2005, 2597, 1932, 101, 3528, 1698, 3663, 900, 3298, 1872, 1179, 3987, 3695, 3561, 1762, 3785, 3005, 2574, 6, 1524, 2738, 1753, 2350, 558, 800, 3782, 722, 886, 2176, 3050, 221, 1925, 564, 1271, 2535, 3113, 1310, 2098, 3011, 964, 3281, 6, 1326, 741, 189, 2632, 373, 1176, 548, 64, 1445, 2376, 1524, 2690, 1316, 2304, 1336, 2257, 3227, 2542, 3911, 3460]
LTC = np.zeros([n, m], dtype=(int))
LTC[0,:] = IVK
for i in range(1, n):
for j in range(m // n + 1):
LTC[i,j*n:(j+1)*n] = np.roll(IVK[j*n:(j+1)*n], i)
for _ in range(5):
pr(border, "Give me your salt: ")
SALT = sc()[:-1]
SALT = pad(SALT, m // 4)
MASKED_FLAG = chaffy_mask(SALT, LTC, m, n)
pr(border, f'masked_flag = {MASKED_FLAG}')
if __name__ == '__main__':
main()
Đại khái bài này mình nhập vô một chuỗi bất kì sau đó nó sẽ kiểm tra và pad cái chuỗi mình nhập cho đủ $128$ bytes. Tiếp theo nó chia cái chuỗi làm $2$ phần bằng nhau và thực hiện hàng loạt các bước tính toán để sinh ra $2$ vector $k_{1}$ và $k_{2}$, cuối cùng kết quả trả về sẽ là $flag \oplus k_{1} \oplus k_{2}$.
Điều “bất thường” ở bài này là nếu ta nhập chuỗi ban đầu có độ dài đúng bằng $128$ và khi chia chuỗi đó làm đôi thì ta được $2$ chuỗi khác nhau. Lúc này ta sẽ loại bỏ được các phần random padding lúc check length mà hoàn toàn tự implement để gen ra hai cái $k_{1}$ và $k_{2}$ lúc này chỉ việc xor ngược lại là ra $flag$ thôi =))
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
import numpy as np
def byte_xor(a, b):
return bytes(_a ^ _b for _a,_b in zip(a,b))
def sol(salt, LTC, m, n, ct):
q = n ** 2
half1_salt = salt[:m // 8]
half2_salt = salt[m // 8:]
xor_salts = int.from_bytes(byte_xor(half1_salt, half2_salt), "big")
if xor_salts == 0:
half1_salt = byte_xor(half1_salt, os.urandom(m))
half1_binStr = "{:08b}".format(int(half1_salt.hex(),16))
if(len(half1_binStr) < m):
half1_binStr = "0" * (m - len(half1_binStr)%m) + half1_binStr
half2_binStr = "{:08b}".format(int(half2_salt.hex(),16))
if(len(half2_binStr) < m):
half2_binStr = "0" * (m - len(half2_binStr)%m) + half2_binStr
vec_1 = np.array(list(half1_binStr), dtype=int)
vec_1 = np.reshape(vec_1, (m,1))
vec_2 = np.array(list(half2_binStr), dtype=int)
vec_2 = np.reshape(vec_2, (m,1))
out_1 = LTC.dot(vec_1) % q
out_2 = LTC.dot(vec_2) % q
ct = np.array([x for x in ct])
ct = np.reshape(ct, (n,1))
flag = (ct ^ out_1 ^ out_2) % 256
flag = np.reshape(flag, (n, ))
print(bytes(list(flag)))
m, n = 512, 64
IVK = [3826, 476, 3667, 2233, 1239, 1166, 2119, 2559, 2376, 1208, 2165, 2897, 830, 529, 346, 150, 2188, 4025, 3667, 1829, 3987, 952, 3860, 2574, 959, 1394, 1481, 2822, 3794, 2950, 1190, 777, 604, 82, 49, 710, 1765, 3752, 2970, 952, 803, 873, 2647, 2643, 1096, 1202, 2236, 1492, 3372, 2106, 1868, 535, 161, 3143, 3370, 1, 1643, 2147, 2368, 3961, 1339, 552, 2641, 3222, 2505, 3449, 1540, 2024, 618, 1904, 314, 1306, 3173, 4040, 1488, 1339, 2545, 2167, 394, 46, 3169, 897, 4085, 4067, 3461, 3444, 118, 3185, 2267, 3239, 3612, 2775, 580, 3579, 3623, 1721, 189, 650, 2755, 1434, 35, 3167, 323, 589, 3410, 652, 2746, 2787, 3665, 828, 3200, 1450, 3147, 720, 3741, 1055, 505, 2929, 1423, 3629, 3, 1269, 4066, 125, 2432, 3306, 4015, 2350, 2154, 2623, 1304, 493, 763, 1765, 2608, 695, 30, 2462, 294, 3656, 3231, 3647, 3776, 3457, 2285, 2992, 3997, 603, 2342, 2283, 3029, 3299, 1690, 3281, 3568, 1927, 2909, 1797, 1675, 3245, 2604, 1272, 1146, 3301, 13, 3712, 2691, 1097, 1396, 3694, 3866, 2066, 1946, 3476, 1182, 3409, 3510, 2920, 2743, 1126, 2154, 3447, 1442, 2021, 1748, 1075, 1439, 3932, 3438, 781, 1478, 1708, 461, 50, 1881, 1353, 2959, 1225, 1923, 1414, 4046, 3416, 2845, 1498, 4036, 3899, 3878, 766, 3975, 1355, 2602, 3588, 3508, 3660, 3237, 3018, 1619, 2797, 1823, 1185, 3225, 1270, 87, 979, 124, 1239, 1763, 2672, 3951, 984, 869, 3897, 327, 912, 1826, 3354, 1485, 2942, 746, 833, 3968, 1437, 3590, 2151, 1523, 98, 164, 3119, 1161, 3804, 1850, 3027, 1715, 3847, 2407, 2549, 467, 2029, 2808, 1782, 1134, 1953, 47, 1406, 3828, 1277, 2864, 2392, 3458, 2877, 1851, 1033, 798, 2187, 54, 2800, 890, 3759, 4085, 3801, 3128, 3788, 2926, 1983, 55, 2173, 2579, 904, 1019, 2108, 3054, 284, 2428, 2371, 2045, 907, 1379, 2367, 351, 3678, 1087, 2821, 152, 1783, 1993, 3183, 1317, 2726, 2609, 1255, 144, 2415, 2498, 721, 668, 355, 94, 1997, 2609, 1945, 3011, 2405, 713, 2811, 4076, 2367, 3218, 1353, 3957, 2056, 881, 3420, 1994, 1329, 892, 1577, 688, 134, 371, 774, 3855, 1461, 1536, 1824, 1164, 1675, 46, 1267, 3652, 67, 3816, 3169, 2116, 3930, 2979, 3166, 3944, 2252, 2988, 34, 873, 1643, 1159, 2822, 1235, 2604, 888, 2036, 3053, 971, 1585, 2439, 2599, 1447, 1773, 984, 261, 3233, 2861, 618, 465, 3016, 3081, 1230, 1027, 3177, 459, 3041, 513, 1505, 3410, 3167, 177, 958, 2118, 326, 31, 2663, 2026, 2549, 3026, 2364, 1540, 3236, 2644, 4050, 735, 280, 798, 169, 3808, 2384, 3497, 1759, 2415, 3444, 1562, 3472, 1151, 1984, 2454, 3167, 1538, 941, 1561, 3071, 845, 2824, 58, 1467, 3807, 2191, 1858, 106, 3847, 1326, 3868, 2787, 1624, 795, 3214, 1932, 3496, 457, 2595, 3043, 772, 2436, 2160, 3428, 2005, 2597, 1932, 101, 3528, 1698, 3663, 900, 3298, 1872, 1179, 3987, 3695, 3561, 1762, 3785, 3005, 2574, 6, 1524, 2738, 1753, 2350, 558, 800, 3782, 722, 886, 2176, 3050, 221, 1925, 564, 1271, 2535, 3113, 1310, 2098, 3011, 964, 3281, 6, 1326, 741, 189, 2632, 373, 1176, 548, 64, 1445, 2376, 1524, 2690, 1316, 2304, 1336, 2257, 3227, 2542, 3911, 3460]
LTC = np.zeros([n, m], dtype=(int))
LTC[0,:] = IVK
for i in range(1, n):
for j in range(m // n + 1):
LTC[i,j*n:(j+1)*n] = np.roll(IVK[j*n:(j+1)*n], i)
# nc 65.21.255.31 31377
salt = b'11111111111111111111111111111111111111111111111111111111111111112222222222222222222222222222222222222222222222222222222222222222'
ct = bytes.fromhex("d6c0efa625303d39e3fac590011e3d3ef2f7f99d3f0f3412f4fcca99370f3522f9cccf81010b3d3ec8e0c99a31133322f8fcc99a31133322f8ccc3942d257d30")
sol(salt, LTC, m, n, ct)
Flag:
ASIS{Lattice_based_hash_collision_it_was_sooooooooooooooo_easY!}
Mariana (59 solves, 80 points)
Description
Mariana works in the areas of cryptography and security. But some flaws exists in her work!
nc 65.21.255.31 32066Attachments
mariana.py
Challenge overview
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
#!/usr/bin/env python3
from Crypto.Util.number import *
import sys
from flag import flag
def die(*args):
pr(*args)
quit()
def pr(*args):
s = " ".join(map(str, args))
sys.stdout.write(s + "\n")
sys.stdout.flush()
def sc():
return sys.stdin.buffer.readline()
def main():
border = "|"
pr(border*72)
pr(border, "Welcome to MARIANA cryptography battle, the mission is solving super", border)
pr(border, "hard special DLP problem in real world, are you ready to fight? ", border)
pr(border*72)
NBIT = 32
STEP = 40
pr(border, "In each step solve the given equation and send the solution for x. ", border)
c = 1
while c <= STEP:
nbit = NBIT * c
p = getPrime(nbit)
g = getRandomRange(3, p)
pr(border, f'p = {p}')
pr(border, f'g = {g}')
pr(border, 'Send the solution x = ')
ans = sc()
try:
x = int(ans)
except:
die(border, 'Given number is not integer!')
if x >= p:
die(border, "Kidding me!? Your solution must be smaller than p :P")
if (pow(g, x, p) - x) % p == 0:
if c == STEP:
die(border, f"Congratz! the flag is: {flag}")
else:
pr(border, "Good job, try to solve the next level!")
c += 1
else:
die(border, "Try harder and smarter to find the solution!")
if __name__ == '__main__':
main()
Bài này bắt chúng ta giải phương trình:
\[g^{x} = x \pmod{p}\]với $p$ là số nguyên tố, $g \in (3, p)$. Nhiệm vụ của ta là tìm $x$ và pass qua $40$ rounds (sau mỗi round $p$ sẽ tăng dần) để lấy flag. Sau một hồi lựa chọn thì thật bất ngờ mình thấy 1 họ nghiệm thỏa yêu cầu đề đơn giản như sau:
Khi đó
\[g^{x} = g^{1} = g = x \pmod{p}\]Một vấn đề nho nhỏ là nếu tính $crt([1, g], [p - 1, p])$ thì kết quả sẻ lớn hơn $p$, nhưng đề chỉ giới hạn $x < p$ chứ không quan tâm cận dưới của $x$ nếu lúc nay chỉ việc “dịch xuống” 1 bậc: $x = crt([1, g], [p - 1, p]) - p(p - 1)$ là sẽ thỏa!
Solution
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
from sage.all import *
from pwn import *
def sol():
io.recvuntil(b'| p = ')
p = int(io.recvline())
io.recvuntil(b'| g = ')
g = int(io.recvline())
x = crt([1, g], [p - 1, p]) - p*(p - 1)
io.sendlineafter(b'| Send the solution x = \n', str(x).encode())
print(io.recvline())
io = remote("65.21.255.31", 32066)
for i in range(40):
sol()
Flag:
ASIS{fiX3d_pOIn7s_f0r_d!5Cret3_l0g4riThmS!}
Mindseat (33 solves, 128 points)
Description
Cryptography Mindset: Be Unpredictable, build robust and stable applications where you’ll handle every situation that user can face or predict.Attachments
mindseat.py output.txt
Ý tưởng bài này như sau: đầu tiên chia flag thành $4$ phần, mỗi phần $8$ bytes, sau đó encrypt từng phần như sau:
Đầu tiên ta sẽ tìm cách khôi phục số $k$…
ở đây ta thấy $k$ sẽ là số mũ đúng $mod 2$ của $n - 1$ nếu $a + b$ lẻ. Vì $a, b$ chọn ngẫu nhiên và ta có tới $4$ bộ pubkey nên khả năng cao sẽ có $1$ bộ mà $a + b$ lẻ, từ đó ta khôi phục được $k = 134$.
Một cách tự nhiên ta sẽ quan tâm tới đại lượng $\phi(n)$…
ở đây ta đã có k vậy thử tìm ab xem…
tới đây ngon rồi!!! Ta đã có thể tính được $\phi(n)$ kết hợp với $n$ ta hoàn toàn tìm được $p, q$. Vậy ta đã xử lý được phần pubkey, bây giờ tìm cách decrypt nữa là xong…
Ở đây $r$ là một số random bất kì, chúng ta không biết. Vậy suy nghĩ một cách tự nhiên là chúng ta sẽ tìm cách loại bỏ $r$ và chuyển sang giải DLP thoy…
Solution
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
from sage.all import *
from Crypto.Util.number import *
PUBKEYS = [(10342840547250370454282840290754052390564265157174829726645242904324433774727630591803186632486959590968595230902808369991240437077297674551123187830095873, 5179654005441544601140101875149402241567866059199512232495766031194848985776186595289740052214499657697650832860279375151687044465018028876445070588827777), (6015512135462554031390611730578383462516861987731833360559070749140159284050335604168414434218196369921956160353365713819898567416920672209509202941444097, 2116441415129068001049624780654272734931672052541246678702416144768611225693039503554945326959705314527114860312641379671935648337975482830939466425225421), (6396980904648302374999086102690071222661654639262566535518341836426544747072554109709902085144158785649143907600058913175220229111171441332366557866622977, 1760317994074087854211747561546045780795134924237097786412713825282874589650448491771874326890983429137451463523250670379970999252639812107914977960011738), (9158217300815233129401608406766983222991414185115152402477702381950519098200234724856258589693986849049556254969769863821366592458050807400542885348638721, 6564146847894132872802575925374338252984765675686108816080170162797938388434600448954826704720292576935713424103133182090390089661059813982670332877677256)]
ENCS = [4595268033054096192076432659360373235610019564489694608733743330870893803828258295069937060360520598446948290913045781945314108935153236291467160667601985, 3390637292181370684803039833768819598968576813582112632809296088618666221278429695211004046274005776653775480723833818255766663573061866194380012311184611, 5197599582013327040903216369733466147938613487439777125659892779696104407398257678982801768761973934713675657188014051286238194316997970299887749668838196, 5093835186720390391696398671365109925058893544530286148616117890366909889206952477053316867658405460457795493886317792695055944930027477761411273933822112]
k = 134
def dlog(a, p, q):
Fp, Fq = GF(p), GF(q)
return crt([discrete_log(Fp(a), Fp(s)), discrete_log(Fq(a), Fq(s))], [p - 1, q - 1])
flag = ''
for (n, s), ct in zip(PUBKEYS, ENCS):
ab = (n - 1)//2**(2*k)
phi = ab * 2**(2*k)
P = PolynomialRing(ZZ, "x")
x = P.gen()
f = x**2 - (n + 1 - phi)*x + n
(p, _), (q, _) = f.roots()
ct = pow(ct, ab, n)
m = dlog(ct, p, q) //ab
flag += long_to_bytes(m).decode()
print('ASIS{' + flag + '}')
Flag:
ASIS{N3w_CTF_nEW_Joye_Libert_CrYpt0_5}
Desired curve (19 solves, 194 points)
Description
nc 65.21.255.31 10101Attachments
desiredcurve.py
Challenge overview
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
#!/usr/bin/env sage
import sys
from Crypto.Util.number import *
from flag import flag
def die(*args):
pr(*args)
quit()
def pr(*args):
s = " ".join(map(str, args))
sys.stdout.write(s + "\n")
sys.stdout.flush()
def sc():
return sys.stdin.buffer.readline()
def main():
border = "|"
pr(border*72)
pr(border, "Hi all, now it's time to solve a relatively simple challenge about ", border)
pr(border, "relatively elliptic curves! We will generate an elliptic curve with ", border)
pr(border, "your desired parameters, are you ready!? ", border)
pr(border*72)
nbit = 256
q = getPrime(nbit)
F = GF(q)
while True:
pr(border, "Send the `y' element of two points in your desired elliptic curve: ")
ans = sc()
try:
y1, y2 = [int(_) % q for _ in ans.split(b',')]
except:
die(border, "Your parameters are not valid! Bye!!")
A = (y1**2 - y2**2 - 1337**3 + 31337**3) * inverse(-30000, q) % q
B = (y1**2 - 1337**3 - A * 1337) % q
E = EllipticCurve(GF(q), [A, B])
G = E.random_point()
m = bytes_to_long(flag)
assert m < q
C = m * G
pr(border, f'The parameters and encrypted flag are:')
pr(border, f'q = {q}')
pr(border, f'G = ({G.xy()[0]}, {G.xy()[1]})')
pr(border, f'm * G = ({C.xy()[0]}, {C.xy()[1]})')
pr(border, f'Now find the flag :P')
if __name__ == '__main__':
main()
Ta được phép chọn 2 số $y_{1}, y_{2}$ sau đó server sẽ sinh ra 1 Curve $(E): y^{2} = x^{3} + Ax + B$ đi qua hai điểm
\[\left(1337, y_{1}\right) \text{ và } \left(31337, y_{2}\right)\]và dùng curve đó để encrypt flag ($m$)
sau cùng server trả về cho ta 2 giá trị $G$ và $mG$.
Ta thấy curve được sinh ngẫu nhiên theo các tham số $A, B$ (mình control được) và $q$ (số nguyên tố ngẫu nhiên do server random) nên ta không thể trông chờ xảy ra trường hợp curve được sinh ra có order smooth hoàn toàn (ví dụ factor của order $< 2^{25}$) để tính trực tiếp discrete_log (tính 1 phát ra flag luôn)
Thay vào đó, ta nên tận dụng các trường hợp curve có order chứa các ước nhỏ (curve tồn tại subgroup có order smooth) và sau đó tính $m$ tên từng subgroup đó, sau cùng flag được tổng hợp lại bằng CRT
Solution
Như vậy ta sẽ connect tới server nhiều lần, mỗi lần tính $m$ trên subgroup và tổng hợp kết quả từng lần tính lại bằng CRT cho tới khi xuất hiện 'ASIS' trong flag thì dừng
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
from sage.all import *
from pwn import *
from Crypto.Util.number import long_to_bytes, inverse
from factordb.factordb import *
class Challenge:
def __init__(self, HOST, PORT):
self.io = process(["python3", "chall.py"])
def getCurve(self):
y1, y2 = [getrandbits(10) for _ in range(2)]
self.io.sendlineafter(b':', f'{y1},{y2}'.encode())
self.io.recvuntil(b'| q = ')
q = int(self.io.recvline())
A = (y1**2 - y2**2 - 1337**3 + 31337**3) * inverse(-30000, q) % q
B = (y1**2 - 1337**3 - A * 1337) % q
E = EllipticCurve(GF(q), [A, B])
self.io.recvuntil(b'| G = ')
G = E.point([int(x) for x in self.io.recvline()[1:-2].split(b', ')])
self.io.recvuntil(b'| m * G = ')
mG = E.point([int(x) for x in self.io.recvline()[1:-2].split(b', ')])
self.io.close()
return [G, mG]
def smallFactor(p, B=2**25):
res = 1
for _ in range(10):
f = FactorDB(p); f.connect()
factor_list = list(f.get_factor_list())
if len(factor_list) > 1:
break
for pr in factor_list:
if pr < B: res *= pr
return res
if __name__ == '__main__':
Ms, Qs = [], []
while True:
chall = Challenge("65.21.255.31", 10101)
G, mG = chall.getCurve()
q = G.order()
subq = smallFactor(q)
if subq == 1: continue
info(f"Found small subgroup: {subq}")
m = discrete_log(mG * (q//subq), G * (q//subq), ord=ZZ(subq), operation='+')
Ms.append(m); Qs.append(ZZ(subq))
flag = long_to_bytes(int(crt(Ms, Qs)))
if b'ASIS' in flag:
success(f'Flag: {flag.decode()}')
exit()
Flag:
ASIS{(e$l6LH_JfsJ:~<}1v&}