Cleithrophobia (58 solves, 472 points)
Description
To protect my flag from you I both encrypted AND decrypted it with AES, but differently. Does that make sense? I’m kind of confused myself honestly…
nc cleithrophobia.chal.idek.team 1337Attachments
cleithrophobia.py
Challenge overview
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
#!/usr/bin/env python3
#
# Polymero
#
# Imports
from Crypto.Cipher import AES
from Crypto.Util.Padding import pad, unpad
import os
# Local imports
with open('flag.txt', 'rb') as f:
FLAG = f.read()
f.close()
# Header
HDR = r"""|
|
| __ _ ___ ____ ______ __ __ ____ ___ ____ __ __ ___ ____ ____ ____
| / ] | / _] | | | | \ / \| \| | |/ \| \| |/ |
| / /| | / [_ | || | | | D ) | o ) | | | o )| || o |
| / / | |___/ _]| ||_| |_| _ | /| O | _/| _ | O | || || |
| / \_| | [_ | | | | | | | \| | | | | | | O || || _ |
| \ | | || | | | | | | . \ | | | | | | || || | |
| \____|_____|_____|____| |__| |__|__|__|\_|\___/|__| |__|__|\___/|_____|____|__|__|
|
|"""
# Server encryption function
def encrypt(msg, key):
pad_msg = pad(msg, 16)
blocks = [os.urandom(16)] + [pad_msg[i:i+16] for i in range(0,len(pad_msg),16)]
itm = [blocks[0]]
for i in range(len(blocks) - 1):
tmp = AES.new(key, AES.MODE_ECB).encrypt(blocks[i+1])
itm += [bytes(j^k for j,k in zip(tmp, blocks[i]))]
cip = [blocks[0]]
for i in range(len(blocks) - 1):
tmp = AES.new(key, AES.MODE_ECB).decrypt(itm[-(i+1)])
cip += [bytes(j^k for j,k in zip(tmp, itm[-i]))]
return b"".join(cip[::-1])
# Server connection
KEY = os.urandom(32)
print(HDR)
print("| ~ I trapped the flag using AES encryption and decryption layers, so good luck ~ ^w^")
print(f"|\n| flag = {encrypt(FLAG, KEY).hex()}")
# Server loop
while True:
try:
print("|\n| ~ Want to encrypt something?")
msg = bytes.fromhex(input("|\n| > (hex) "))
enc = encrypt(msg, KEY)
print(f"|\n| {enc.hex()}")
except KeyboardInterrupt:
print('\n|\n| ~ Well goodbye then ~\n|')
break
except:
print('|\n| ~ Erhm... Are you okay?\n|')
Để đơn giản ta ký hiệu $E(x)$ và $D(x)$ lần lượt là các hàm encrypt và decrypt AES.MODE_ECB. Giả sử ta đưa cho server encrypt một message có độ dài $48$ bytes (chia thành các block $B_{i}$) như sau
\[B_{1} \quad || \quad B_{2} \quad || \quad B_{3} \quad || \quad \text{PAD}\]thì server sẽ trả về kết quả sau khi encrypt là
\[D\left(E\left(B_{1}\right) \oplus IV\right) \oplus E\left(B_{2}\right) \oplus B_{1} \quad || \quad D\left(E\left(B_{2}\right) \oplus B_{1}\right) \oplus E\left(B_{3}\right) \oplus B_{2} \quad || \quad D\left(E\left(B_{3}\right) \oplus B_{2}\right) \oplus E\left(PAD\right) \oplus B_{3} \quad || \quad D\left(E\left(PAD\right) \oplus B_{3}\right) \oplus IV\]Để ý rằng nếu ta thay $B_{1} = B_{2} = 0$ và $B_{3}$ bất kỳ thì block thứ $2$ của kết quả trả về sẽ có giá trị
\[\begin{align} D\left(E\left(B_{2}\right) \oplus B_{1}\right) \oplus E\left(B_{3}\right) \oplus B_{2} &= D\left(E\left(0\right) \oplus0\right) \oplus E\left(X\right) \oplus 0 \\ &= D\left(E\left(0\right)\right) \oplus E\left(X\right) \\ &= 0 \oplus E(X) \\ &= E(X) \end{align}\]như vậy ta có thể encrypt MODE_ECB bất kỳ msg nào mà không cần biết KEY, hoàn toàn tương tự cho việc decrypt MODE_ECB. Như vậy việc còn lại khá đơn giản là reverse lại hàm encrypt của server thôi!
Solution
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
from pwn import *
from Crypto.Util.Padding import pad, unpad
def xor(a, b):
return bytes([x^y for x,y in zip(a, b)])
class Solution:
def __init__(self, HOST, PORT) -> None:
# self.io = process(["python3", "chall.py"])
self.io = remote(HOST, PORT)
self.io.recvuntil(b'| flag = ')
self.enc = bytes.fromhex(self.io.recvline()[:-1].decode())
def encrypt(self, msg):
self.io.sendlineafter(b'| > (hex) ', msg.hex().encode())
self.io.recvline()
self.io.recvuntil(b'| ')
ct = bytes.fromhex(self.io.recvline()[:-1].decode())
return [ct[i:i+16] for i in range(0, len(ct), 16)]
def encryptECB(self, msg):
return self.encrypt(b'\0'*32 + msg)[1]
def decryptECB(self, msg):
payload = xor(msg, self.encryptECB(pad(b'', 16)))
ct = self.encrypt(payload)
return xor(ct[-1], ct[-2])
def decrypt(self, enc):
cip = [enc[i:i+16] for i in range(0, len(enc), 16)]
itm = [cip[-1]]
for i in reversed(range(len(cip) - 1)):
tmp = xor(cip[i], itm[-1])
itm += [self.encryptECB(tmp)]
msg = [itm[0]]
itm = itm[1:][::-1]
for i in range(len(itm)):
tmp = xor(itm[i], msg[-1])
msg += [self.decryptECB(tmp)]
return unpad(b''.join(msg[1:]), 16)
def getFlag(self):
return self.decrypt(self.enc)
if __name__ == '__main__':
HOST, PORT = "cleithrophobia.chal.idek.team", 1337
sol = Solution(HOST, PORT)
flag = sol.getFlag()
print(flag)
Flag:
flag{wh0_3v3n_c0m3s_up_w1th_r1d1cul0us_sch3m3s_l1k3_th1s__0h_w41t__1_d0}
ECRSA (40 solves, 481 points)
Description
ECDSA, ECDH, ECwhatever… Through the power of elliptic curves, every cipher can be made stronger. Idek️️️®️ is proud to prevent a new and improved version of RSA, the long-awaited ECRSA™️! This clever variant combines the modern with the classic, the powered with the elliptic, the unbreakable with the strong!
Challenge overview
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
p, q = [random_prime(2^512, lbound = 2^511) for _ in range(2)]
e = 3
while gcd(p - 1, e) != 1: p = next_prime(p)
while gcd(q - 1, e) != 1: q = next_prime(q)
n = p*q
d = inverse_mod(e, (p-1)*(q-1))
# d stands for debug. You don't even know n, so I don't risk anything.
print('d =', d)
m = ZZ(int.from_bytes(b"It is UNBREAKABLE, I tell you!! I'll even bet a flag on it, here it is: idek{REDACTED}", 'big'))
t = ZZ(int.from_bytes(b"ECRSA offers added security by elliptic entropy.", 'big'))
ym = randint(1, n)
yt = 2
# I like it when my points lie on my curve.
a, b = matrix([[m, 1], [t, 1]]).solve_right([ym^2 - m^3, yt^2 - t^3])
E = EllipticCurve(Zmod(n), [a, b])
M = E(m, ym)
T = E(t, yt)
E.base_field = E.base_ring # fix multiplication over rings (might not work depending on sage version!)
print('Encrypted flag:', M*e)
print('Encrypted test:', T*e)
1
2
3
d = 99193023581616109152177764300040037859521925088272985981669959946817746109531909713425474710564402873765914926441545005839662821744603138460681680285655317684469203777533871394260260583839662628325884473084768835902143240687542429953968760669321064892423877370896609497584167478711224462305776836476437268587
Encrypted flag: (115076663389968253954821343472300155800654332223208277786605760890770425514748910251950393842983935903563187546008731344369976804796963863865102277460894378910744413097852034635455187460730497479244094103353376650220792908529826147612199680141743585684118885745149209575053969106545841997245139943766220688789 : 74232642959425795109854140949498935461683632963630260034964643066394703345139733396470958836932831941672213466233486926122670098721687149917605871805886006479766670309639660332339984667770417687192717160061980507220617662938436637445370463397769213554349920956877041619061811087875024276435043752581073552318 : 1)
Encrypted test: (79615329406682121028641446306520032869660130854153788352536429332441749473394735222836513266191300847548366008281109415002581029448905418880962931523411475044527689429201653146200630804486870653795937020571749192405439450656659472253086567149309166068212312829071678837253421625687772396105149376211148834937 : 114576105009077728778286635566905404081211824310970349548035698466418670695753458926421098950418414701335730404414509232776047250916535638430446206810902182305851611221604003509735478943147034397832291215478617613443375140890349118302843641726392253137668650493281241262406250679891685430326869028996183320982 : 1)
Đầu tiên đề sinh ra bộ RSA key $(n, e, d)$ và cho ta giá trị của $d$. Tiếp theo đề chọn $2$ điểm
\[M(m, y_{m}) \text{ và } T(t, 2)\]trong đó $M$ là điểm ta không biết tọa độ và ta cần tìm nó (hoành độ điểm $M$ có chứa flag) còn $T$ là điểm ta đã biết đầy đủ tọa độ. Sau đó tính giá trị $a, b$ của Curve đi qua 2 điểm trên
cuối cùng trả về cho ta hai giá trị $3 \times E(M)$ và $3 \times E(T)$
Recover curve’s parameters
Việc đầu tiên cần làm là tìm ra các tham số của curve $(n, a, b)$. Đầu tiên ta đã có $3$ điểm thuộc curve $(T, 3\times M, 3\times T)$, ta ký hiệu:
\[3\times T: \left(x_{T}, y_{T}\right) \text{ và } 3\times M: \left(x_{M}, y_{M}\right)\]khi đó ta dễ dàng tìm được $a, b$ trên $\mathbb{Q}$ bằng cách giải hệ sau
\[\begin{bmatrix} y_{M}^{2} - x_{M}^{3} \\ y_{T}^{2} - x_{T}^{3} \end{bmatrix} = \begin{bmatrix} x_{M} & 1 \\ x_{T} & 1 \end{bmatrix} \begin{bmatrix} a \\ b \end{bmatrix}\]Có được $a, b$ rồi thì ta tính toán trên curve như bình thường (chỉ trừ phép $mod$ là chưa tính được vì chưa biết $n$). Lúc này ta thế ngược tọa độ hai điểm $T$ và $3 \times T$ vào để tính $\gcd$ và dễ dàng thu được giá trị chính xác của $n$
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
from sage.all import *
from factordb.factordb import *
def onCurve(a, b, P):
return P[0]**3 + a*P[0] + b - P[1]**2
_3M = (115076663389968253954821343472300155800654332223208277786605760890770425514748910251950393842983935903563187546008731344369976804796963863865102277460894378910744413097852034635455187460730497479244094103353376650220792908529826147612199680141743585684118885745149209575053969106545841997245139943766220688789, 74232642959425795109854140949498935461683632963630260034964643066394703345139733396470958836932831941672213466233486926122670098721687149917605871805886006479766670309639660332339984667770417687192717160061980507220617662938436637445370463397769213554349920956877041619061811087875024276435043752581073552318)
_3T = (79615329406682121028641446306520032869660130854153788352536429332441749473394735222836513266191300847548366008281109415002581029448905418880962931523411475044527689429201653146200630804486870653795937020571749192405439450656659472253086567149309166068212312829071678837253421625687772396105149376211148834937, 114576105009077728778286635566905404081211824310970349548035698466418670695753458926421098950418414701335730404414509232776047250916535638430446206810902182305851611221604003509735478943147034397832291215478617613443375140890349118302843641726392253137668650493281241262406250679891685430326869028996183320982)
T = (ZZ(int.from_bytes(b"ECRSA offers added security by elliptic entropy.", 'big')), 2)
a, b = matrix(QQ, [
[_3M[0], 1],
[_3T[0], 1]
]).solve_right(vector([_3M[1]**2 - _3M[0]**3, _3T[1]**2 - _3T[0]**3]))
kN = gcd(onCurve(a, b, T), onCurve(a, b, _3T)).numerator()
# remove trivial factor
f = FactorDB(kN); f.connect()
kn = f.get_factor_list()[-1]
E = EllipticCurve(Zmod(kn), [a, b])
__3T = 3*E.point(T)
n = gcd(_3T[0] - __3T[0], _3T[1] - __3T[1])
print(n)
# 148789535372424163728266646450060056789282887632409478972504939920226619164297864570138212065846604310648872389662317508759494232616904707691022520428483000923260778669946008689451863137527523684502948570798504215922534787506491833325381174139925947167122783344470619692746866285435276907642606269209931602317
Factorize modulo n
Sau kết quả $n$ tìm được ở trên, ta đã biết được bộ $(n, e, d)$ thỏa mãn
\[ed - 1 \equiv 0 \pmod{\Phi\left(n\right)}\]vì $d \sim \Phi\left(n\right)$ mà $e = 3$ (khá bé), nên ta hoàn toàn tính được chính xác (brute force) giá trị của $Phi\left(n\right)$, kết hợp với $n$ dễ dàng tìm được $p, q$
1
2
3
4
5
6
7
8
9
10
11
12
13
14
from sage.all import *
e = 3
d = 99193023581616109152177764300040037859521925088272985981669959946817746109531909713425474710564402873765914926441545005839662821744603138460681680285655317684469203777533871394260260583839662628325884473084768835902143240687542429953968760669321064892423877370896609497584167478711224462305776836476437268587
n = 148789535372424163728266646450060056789282887632409478972504939920226619164297864570138212065846604310648872389662317508759494232616904707691022520428483000923260778669946008689451863137527523684502948570798504215922534787506491833325381174139925947167122783344470619692746866285435276907642606269209931602317
for k in range(1, 3):
phi = (e*d - 1)//k
Px = PolynomialRing(ZZ, "x"); x = Px.gen()
f = x**2 - (n + 1 - phi)*x + n
if f.roots():
(p, _e1), (q, _e2) = f.roots()
break
print(p, q)
# 12290271213546041363951851773787980582602437964255454723585180242187866091592878156042540239644364150942318226563612517243038643884916020981628688069132457 12106285759457603837646209698473787447139576157605716627376889077738609086595516271990595704705464336024969899141833853372028724555298162959385807206566981
Tới đây công việc cuối cùng là giải ECDLP để tìm flag thui
Solution
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
from sage.all import *
from factordb.factordb import *
from Crypto.Util.number import long_to_bytes
def onCurve(a, b, P):
return P[0]**3 + a*P[0] + b - P[1]**2
_3M = (115076663389968253954821343472300155800654332223208277786605760890770425514748910251950393842983935903563187546008731344369976804796963863865102277460894378910744413097852034635455187460730497479244094103353376650220792908529826147612199680141743585684118885745149209575053969106545841997245139943766220688789, 74232642959425795109854140949498935461683632963630260034964643066394703345139733396470958836932831941672213466233486926122670098721687149917605871805886006479766670309639660332339984667770417687192717160061980507220617662938436637445370463397769213554349920956877041619061811087875024276435043752581073552318)
_3T = (79615329406682121028641446306520032869660130854153788352536429332441749473394735222836513266191300847548366008281109415002581029448905418880962931523411475044527689429201653146200630804486870653795937020571749192405439450656659472253086567149309166068212312829071678837253421625687772396105149376211148834937, 114576105009077728778286635566905404081211824310970349548035698466418670695753458926421098950418414701335730404414509232776047250916535638430446206810902182305851611221604003509735478943147034397832291215478617613443375140890349118302843641726392253137668650493281241262406250679891685430326869028996183320982)
T = (ZZ(int.from_bytes(b"ECRSA offers added security by elliptic entropy.", 'big')), 2)
a, b = matrix(QQ, [
[_3M[0], 1],
[_3T[0], 1]
]).solve_right(vector([_3M[1]**2 - _3M[0]**3, _3T[1]**2 - _3T[0]**3]))
kN = gcd(onCurve(a, b, T), onCurve(a, b, _3T)).numerator()
# remove trivial factor
f = FactorDB(kN); f.connect()
kn = f.get_factor_list()[-1]
E = EllipticCurve(Zmod(kn), [a, b])
__3T = 3*E.point(T)
n = ZZ(gcd(_3T[0] - __3T[0], _3T[1] - __3T[1]))
e = 3
d = 99193023581616109152177764300040037859521925088272985981669959946817746109531909713425474710564402873765914926441545005839662821744603138460681680285655317684469203777533871394260260583839662628325884473084768835902143240687542429953968760669321064892423877370896609497584167478711224462305776836476437268587
for k in range(1, 3):
phi = (e*d - 1)//k
Px = PolynomialRing(ZZ, "x"); x = Px.gen()
f = x**2 - (n + 1 - phi)*x + n
if f.roots():
(p, _e1), (q, _e2) = f.roots()
assert is_prime(p) and is_prime(q)
break
Ep, Eq = EllipticCurve(GF(p), [a, b]), EllipticCurve(GF(q), [a, b])
_3Mp, _3Mq = Ep.point(_3M), Eq.point(_3M)
# OrEp, OrEq = _3Mp.order(), _3Mq.order()
OrEq = 12106285759457603837646209698473787447139576157605716627376889077738609086595367760906757844814552719704303248523074103662114018990337565151986764666812769
OrEp = 12290271213546041363951851773787980582602437964255454723585180242187866091592930408418132906142473580819234492550892403489633401195027564397193372497063650
mp = (pow(e, -1, OrEp)*_3Mp).xy()[0]
mq = (pow(e, -1, OrEq)*_3Mq).xy()[0]
m = crt([ZZ(mp), ZZ(mq)], [p, q])
print(long_to_bytes(int(m)))
Flag:
idek{Sh3_s3ll5_5n4k3_01l_0n_7h3_5e4_5h0r3}
Megalophobia
Description
My own PRNG is MEGA sus, so I would like to borrow some entropy from you please. I can trust you not to steal my flag, right?… Right?
nc megalophobia.chal.idek.team 1337Attachments
megalophobia.py
Challenge overview
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
#!/usr/bin/env python3
#
# Polymero
#
# Imports
from Crypto.Cipher import AES
from Crypto.Util.number import getPrime, inverse
import os
# Local imports
with open('flag.txt', 'rb') as f:
FLAG = f.read()
f.close()
# Header
HDR = r"""|
|
| ____ ____ ________ ______ _ _____ ___ _______ ____ ____ ___ ______ _____ _
| |_ \ / _|_ __ |.' ___ | / \ |_ _| .' `.|_ __ \_ || _|.' `.|_ _ \|_ _| / \
| | \/ | | |_ \_/ .' \_| / _ \ | | / .-. \ | |__) || |__| | / .-. \ | |_) | | | / _ \
| | |\ /| | | _| _| | ____ / ___ \ | | _| | | | | ___/ | __ | | | | | | __'. | | / ___ \
| _| |_\/_| |_ _| |__/ \ `.___] |_/ / \ \_ _| |__/ \ `-' /_| |_ _| | | |_\ `-' /_| |__) || |_ _/ / \ \_
| |_____||_____|________|`._____.'|____| |____|________|`.___.'|_____| |____||____|`.___.'|_______/_____|____| |____|
|
|"""
# Private RSA key
d = 1
while d == 1:
p, q = [getPrime(512) for _ in '01']
d = inverse(0x10001, (p - 1)*(q - 1))
# Key encoding
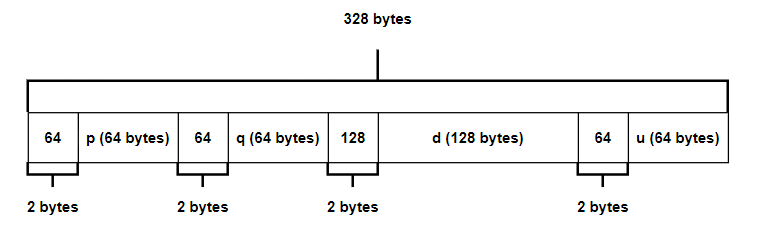
num_byt = [i.to_bytes(256, 'big').lstrip(b'\x00') for i in [p, q, d, inverse(q, p)]]
sec_key = b''.join([len(k).to_bytes(2, 'big') + k for k in num_byt])
# OTP key to encrypt private part
otp_key = os.urandom((len(sec_key) - len(FLAG)) // 2) + b"__" + FLAG + b"__" + os.urandom(-((len(FLAG) - len(sec_key)) // 2))
pub_key = (p * q).to_bytes(128,'big')
enc_key = bytes([i^j for i,j in zip(sec_key, otp_key)])
# Server connection
print(HDR)
print("| ~ Here hold my RSA key pair for me, don't worry, I encrypted the private part ::")
print('| ' + pub_key.hex() + '::' + enc_key.hex())
print("|\n| --- several hours later ---")
print('|\n| ~ Hey, could you send me my encrypted private key?')
# Retrieve private key
try:
my_enc_key = bytes.fromhex(input('|\n| > (hex)'))
my_sec_key = bytes([i^j for i,j in zip(my_enc_key, otp_key)])
pop_lst = []
while len(my_sec_key) >= 2:
pop_len = int.from_bytes(my_sec_key[:2], 'big')
if pop_len <= len(my_sec_key[2:]):
pop_lst += [int.from_bytes(my_sec_key[2:2 + pop_len], 'big')]
my_sec_key = my_sec_key[2 + pop_len:]
else:
my_sec_key = b""
assert len(pop_lst) == 4
p, q, d, u = pop_lst
assert p * q == int.from_bytes(pub_key, 'big')
except:
print("|\n| ~ Erhm... That's not my key? I'll go somewhere else for now, bye...\n|")
exit()
# RSA-CRT decryption function
def decrypt(cip, p, q, d, u):
dp = d % (p - 1)
dq = d % (q - 1)
mp = pow(int.from_bytes(cip, 'big'), dp, p)
mq = pow(int.from_bytes(cip, 'big'), dq, q)
t = (mp - mq) % p
h = (t * u) % p
m = (h * q + mq)
return m.to_bytes(128, 'big').lstrip(b'\x00')
# Game
print("| ~ Now, I don't trust my own PRNG. Could you send me some 128-byte nonces encrypted with my RSA public key?")
for _ in range(500):
enc_rng = bytes.fromhex(input('| > '))
nonce = decrypt(enc_rng, p, q, d, u)
if len(nonce) < 128:
print("| ~ Erhm... are you sure this is a random 128-byte nonce? This doesn't seem safe to me... Q_Q")
else:
print("| ~ Thanks, this looks random ^w^")
Phân tích kĩ source xem sao, đầu tiên server gen bộ RSA private key $(p, q, d, u)$ sau encoding bộ key này thành
sau đó encrypt bộ key này bằng cách xor nó với một cái otp_key được sinh ngẫu nhiên trong đó có 1 phần chứa flag
sau đó server cho ta biết $\text{enc_key}$ và $\text{pub_key}$ (là $p\times q$). Tới đây ta hình dung được nhiệm vụ cần làm là khôi phục bộ private key từ đó tìm được flag trong $\text{otp_key}$.
Tiếp theo server sẽ cho ta tự nhập $\text{enc_key}$, giải mã nó và thu được bộ key $(p, q, d, u)$. Server sẽ dùng bộ key này để thực hiện RSA CRT decryption, ta được phép decrypt $500$ lần và server sẽ check xem kết quả sau khi decrypt có độ dài bé hơn $128$ bytes hay không
Ta xem xét phần nhập $\text{enc_key}$ có control được gì không
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
# Retrieve private key
try:
my_enc_key = bytes.fromhex(input('|\n| > (hex)'))
my_sec_key = bytes([i^j for i,j in zip(my_enc_key, otp_key)])
pop_lst = []
while len(my_sec_key) >= 2:
pop_len = int.from_bytes(my_sec_key[:2], 'big')
if pop_len <= len(my_sec_key[2:]):
pop_lst += [int.from_bytes(my_sec_key[2:2 + pop_len], 'big')]
my_sec_key = my_sec_key[2 + pop_len:]
else:
my_sec_key = b""
assert len(pop_lst) == 4
p, q, d, u = pop_lst
assert p * q == int.from_bytes(pub_key, 'big')
except:
print("|\n| ~ Erhm... That's not my key? I'll go somewhere else for now, bye...\n|")
exit()
Đọc $2$ bytes đầu tiên $\rightarrow$ đổi sang int có giá trị là $l$ $\rightarrow$ đọc $l$ bytes tiếp theo sẽ là giá trị của private key. Như vậy nếu mình flip bit ở các vị trí đọc length thì sẽ sửa được private key từ đó trở về sau. Tuy nhiên ta chỉ sử được giá trị từ $d$ thôi mà không sử được $p, q$ vì có đoạn check
1
assert p * q == int.from_bytes(pub_key, 'big')
Để biết cần điều chỉnh $d, u$ như thế nào thì ta cần phân tích RSA CRT decryption
1
2
3
4
5
6
7
8
9
10
# RSA-CRT decryption function
def decrypt(cip, p, q, d, u):
dp = d % (p - 1)
dq = d % (q - 1)
mp = pow(int.from_bytes(cip, 'big'), dp, p)
mq = pow(int.from_bytes(cip, 'big'), dq, q)
t = (mp - mq) % p
h = (t * u) % p
m = (h * q + mq)
return m.to_bytes(128, 'big').lstrip(b'\x00')
ta thấy, nếu $cip = x^{e} \pmod{n}$ với $x < \min(p, q)$ thì kết quả $m = h\times q + mq$ sẽ đúng bằng $x$ bất kể giá trị nào của $u$ vì khi $x < \min(p, q)$ thì $mp = mq = x \rightarrow t = 0 \rightarrow u$ biến mất!
Tới đây ta nghĩ đến hướng attack như sau: đâu tiên fake cái $\text{enc_key}$ để cho server decrypt ra bộ key $(p, q, d, u’)$ với $u’$ là giá trị sai. Sau đó ta gửi giá trị $x^{e} \mod n$ để server decrypt
- Nếu $x < \min(p, q)$ thì decrypt thành công, kết quả server check được là $< 128$ bytes
- Nếu $x > \min(p, q)$ (hơi nhỉnh hơn) thì decrypt thất bại, nó sẽ ra kết quả bất kỳ, và khả năng cao server sẽ check được là $\ge 128$ bytes. Lý do bởi vì nó sẽ trả về
mà $u’$ mình fake cho nó sai thì $h \times q \sim 2^{1024}$.
Vậy dùng binary search sẽ ok đó, $p, q$ $512$ bit và mình được check $500$ lần thì brute force thêm xíu nữa sẽ tìm được $p, q$ thôi
Solution
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
from sage.all import *
from pwn import *
from Crypto.Util.number import *
def encrypt(m, n):
return long_to_bytes(pow(m, 0x10001, n)).hex().encode()
def keyEncoding(p, q):
d = inverse(0x10001, (p - 1)*(q - 1))
num_byt = [i.to_bytes(256, 'big').lstrip(b'\x00') for i in [p, q, d, inverse(q, p)]]
return b''.join([len(k).to_bytes(2, 'big') + k for k in num_byt])
if __name__ == '__main__':
HOST, PORT = "megalophobia.chal.idek.team", 1337
# io = process(["python3", "chall.py"])
io = remote(HOST, PORT)
io.recvuntil(b"| ~ Here hold my RSA key pair for me, don't worry, I encrypted the private part ::\n| ")
data = io.recvline()[:-1].decode()
pub_key, enc_key = [bytes.fromhex(x) for x in data.split('::')]
n = bytes_to_long(pub_key)
# 2 || p (64 bytes) || 2 || q (64 bytes) || 2 || d (128 bytes) || u (64 bytes)
lenu_pos = (2 + 64)*2 + 2 + 128 + 1
fake_enc_key = enc_key[:lenu_pos] + bytes([enc_key[lenu_pos] ^ 64 ^ 63]) + enc_key[lenu_pos + 1:]
io.sendlineafter(b"> (hex)", fake_enc_key.hex())
lo, hi = 2**511, 2**512 - 1
for _ in range(500):
mid = (lo + hi)//2
io.sendlineafter(b'| > ', encrypt(mid, n))
if b'Erhm' in io.recvline():
lo = mid + 1
else:
hi = mid - 1
for p in range(lo, hi):
if n%p == 0:
q = n//p
sec_key = keyEncoding(p, q)
msg = xor(sec_key, enc_key)
assert b'idek' in msg
print(msg)
Flag:
idek{M3G4_r34lly_n33d_t0_g3t_th3ir_sh1t_t0g3th3r}